Kurt Gödel's Ontological Argument - Part II
Anselm's ontological argument
It is a common conceit of our secular technological age that all medieval
clerics were close-minded. Our picture of medieval monastic
life reinforces that idea. We imagine some monk sitting in a darkened
monastery endlessly reciting the aged dogmas of an ancient religion, and
trapped in a social order that permitted no mobility.
In truth, however,
universities were started in Europe during the medieval period.
Many of the principles of freedom of thought and speech were developed
from the desire of early universities to maintain some independence from
the authoritarian powers of the time.
Whatever validity there is to our picture of the Middle Ages,
derived in part from movies, television and medieval romance literature,
it is a vast oversimplification of
the reality.
The Middle Ages spanned a large stretch of time. To lump all these societies
together would be comparable to confusing Jane Austen's England with
Bill Gates' America. Moreover, many of the ideas we have about
ecclesiastical institutions derive not from the Middle Ages, but from the
dynamic changes of the Reformation and Counter-Reformation.
Certainly there was not the clear line between the sacred and the secular as
exists today. But it was not so much
that ordinary life was more sacred. It was that ecclesiastical
institutions were more secular. Violence was endemic to the society of the
central Middle Ages, with much of the power in the hands of people who were
actually local warlords. The justification for violence was not arbitrary,
but was determined by the authority of the person who committed it. During
Anselm's time the great cathedrals of Europe had yet to be built. But the
need for fortified wooden structures was great, as banditry of one regional
warlord against another (and his serfs) was commonplace.
In education, there was also no division of church and state as exists today.
For a person of intelligence to receive a good education, it was necessary
to be within the ecclesiastical structures and not an outsider.
Thus the dividing lines between philosophers, scientists and theologians
was not as great as in modern times. Opportunities were greater by far for
men. However,
anyone who has read the biography
(Historia Calamitatum)
of Peter Abelard (1101-1164),
including the story of his tumultuous love affair with
Heloise, knows that the love of learning by both genders
is not solely a modern concept.
(The reader of the Historia Calamitatum should not confuse the Anselm
of that story with the Anselm who developed the ontological argument.)
We know
from her
letters
that Heloise was well trained in philosophy and logic: her
letter show a keen awareness of the philosophical issues of the time.
Abelard, on the other hand, was a strong believer in the principle that the
true foundation for religion was not unthinking dogma, but vigorous scepticism.
Only a faith founded on the possibility of doubt was worthy of respect in his
eyes.
What can we say about Hildegard of Bingen (1098-1179)? In modern terms, she
might be described as a polymath, i.e., an individual of encyclopaedic
learning and talent, who was a major contributer to three spheres of
medieval culture: art, music and religious writing.
 Anselm of Aosta (1033-1109) should
also be understood in this context. Like Abelard
or Hildegard, Anselm was a brilliant man whose natural vocation was within
the medieval Church. His biographers have referred to the transformation
that he introduced as the "Anselmian revolution." While he is best
known outside ecclesiastical circles for his ontological argument, his
influence on religious writing is every bit as important. Anselm invented a
new form of poetry -- the poetry of personal devotion written in rhymed Latin
with intricate logical structure and antitheses.
Anselm of Aosta (1033-1109) should
also be understood in this context. Like Abelard
or Hildegard, Anselm was a brilliant man whose natural vocation was within
the medieval Church. His biographers have referred to the transformation
that he introduced as the "Anselmian revolution." While he is best
known outside ecclesiastical circles for his ontological argument, his
influence on religious writing is every bit as important. Anselm invented a
new form of poetry -- the poetry of personal devotion written in rhymed Latin
with intricate logical structure and antitheses.
Anselm was born in Aosta, in the kingdom of Burgundy. He entered the abbey of
Notre Dame at Bec, and, at the age of thirty, replaced Lanfranc as prior. In
1078 he became abbot when Herluin died. In 1093 he became Archbishop of
Canterbury, a position he held until his death. However, it is during his
time at Bec that he wrote much of the material for which he is remembered,
including the Prayers and Meditations and the Proslogion.
It is the Proslogion which contains the basic argument for the existence
of God which we know today as the ontological argument.
Calling Anselm's approach to the existence of God the
ontological argument is probably better than calling it the
ontological proof. In order for an argument to be a proof
it must proceed by a sequence of statements each of which
can be deduced from previous statements or can be regarded as axiomatic in
nature. Mathematical proofs, for example, are usually highly convincing, and
leave little room for doubt provided that they are not so complex as to
overwhelm the intellect. Anselm's ontological argument, while very subtle, is
not complex in the sense that, say, Wiles' proof of Fermat's Last Theorem is
complex. Nevertheless, very few people have been converted from atheism or
agnosticism to the theist position by the argument. The reason for this is
that most people who start out as sceptics remain so because they have an
objection to an assumption of the ontological argument or to one of its rules
of deduction. Nor is it only sceptics who have objections. Many religious
thinkers have found the basis for their spiritual lives in personal experience
rather than dry logical argumentation.
Yet the argument has power. The well known religious writer C. S. Lewis,
author of the Narnia children's books and other influential religious
works, was reportedly converted to Christianity by the ontological argument.
Some people have found the ontological argument to be absurd and have dismissed
it. ("Existence," said Immanuel Kant, "is not a predicate.") Others have
found the argument strangely compelling. One thing is certain, however. Those
who would dismiss God as the product of irrational or superstitious
cultures must contend with the intellectual framework that the ontological
argument sets up. There have been many people, both past and present, who have
been drawn to a faith in God, but have found their way blocked by certain
intellectual barriers. For these people, faith has not been enough unless
it was compatible with human reason. If the human heart leads us to God while
the head howls its indignation, then a reconciliation between the two may end
up being the starting point for a valid faith for these individuals. For those
who have no intellectual difficulties with the existence of God, the
ontological argument will probably remain a curiosity and nothing more.
As I argued on the previous page, a determination of the existence or
nonexistence of any individual requires an examination of the essential
properties of that individual. A claim that Santa, for example, does not exist
must be backed up by arguing that wearing a red suit and a white beard
does not make you into Santa Claus.
The same would appear to be true of arguments for the existence or
nonexistence of God. If two people have different beliefs about the
existence of God, are their beliefs contradictory, or do they simply have
different conceptions of God (i.e., God's essence)? Some people feel that
they have outgrown the need for God. For
these people, the Judeo-Christian
God that they grew up with is far too human in characteristics to be more
than a projection of human vanity onto the cosmic canvas. Other people, who
believe in God, agree with this. They feel that God is a constant
towards whom we move with better and better degrees of approximation.
Still other people, who see the Bible as inerrant, argue that the Biblical
passages give us a clear and accurate understanding of God inasmuch as God
has seen fit to be revealed to us. All of these people vary, to a greater
or lesser extent, in their understanding of the essential properties or
essential qualities of God.
One of Anselm's basic
conclusions was that existence is an essential property of God. This
idea is obtained in the Proslogion by deduction from an understanding
of God's essence. The Proslogion does not stop at the
existence of God, but deduces many other attributes as essential to God:
that God is the creator of everything, that God is omnipotent, compassionate
yet beyond passion, limitless and beyond time, and other properties or
attributes. Yet it is for the existence argument that we most remember
Anselm.
The translation of the Proslogion that I shall use is that of
Benedicta Ward, which can be found in the popular Penguin Classics edition
The Prayers and Meditations of Saint Anselm with the Proslogion,
published in 1973. The numbering of verses follows that edition.
Within his introductory passages of the Proslogion, Anselm asks
By what signs, by what forms, shall I seek you [i.e., God]? (27)
I take this question to be an inquiry into the essential qualities [i.e.,
properties] of God, and perhaps an inquiry in the essence of God. Anselm
realises that without some understanding of the essential qualities of God,
God will be completely inaccessible.
We believe you [i.e., God] are that thing than which nothing greater can be
thought. (160)
This is Anselm's famous statement about God. It is either to be understood
as a statement of God's essence, or as a statement about an essential
property of God from which many other essential properties are to be
deduced. The expression "can be thought" is not meant as in the
psychological sense, but as a limitation on possibility: God is that for
which it is impossible that there be a greater being in any respect.
But when the fool hears me use the phrase
"something than which nothing
greater can be thought"
he understands what he hears ... .
So the fool has
to agree that
the concept of something than which nothing greater can be
thought
exists in his understanding (163, 173)
The word "fool" is not to be understood in its modern sense. Anselm means
an atheist by this term. This usage derives from the Bible, in which the
Hebrew word translated as "fool" denotes a morally deficient person, rather
than someone who is stupid in the intellectual sense. Once again, by the
"understanding", Anselm is referring to the modal realm of possibility. That
which exists in the understanding is that which is possible. So Anselm is
asserting that even the atheist would agree that it is possible that God
exists. Even though the atheist asserts that God's existence is false, the
atheist surely would agree that this is a contingent falsehood. Like
a painter who imagines a picture before painting it, the atheist can conceive
of a world in which God exists even if that world is not the true world.
This leads us to the first of Anselm's axioms, namely
Axiom 1:  g
g
where g is the proposition that God exists. When we consider Gödel's
ontological argument, we shall see that this statement will not be taken as
axiomatic. Indeed, Gödel's contribution to the ontological argument is
partly a deeper analysis of this statement, which is axiomatic here. We have
to say that Anselm does provide an argument for Axiom 1. However, his
argument is not convincing, because he does not distinguish between
propositions which are conceivable, and propositions which are
possible. (We take him to mean the latter.) The distinction
is very important. For example, I can conceive of an even integer greater than
two which cannot be written as the sum of two prime numbers. However, the
fact that I can conceive of such an integer does not mean that one possibly
exists. Mathematical objects such as integers
are usually understood as having only essential properties and not
accidental ones.
(At least, this is the usual understanding of the mathematical
Platonist.)
Something than which nothing greater can be thought so truly exists
that
it is not possible to think of it as
not existing (194)
With this statement, Anselm rules out the contingent
(i.e., accidental) existence of a deity.
We can formalize this in modal logic as
Axiom 2: g 
 g
g
Anselm's argument is that if God existed only in a contingent sense, then
we could imagine a greater being, namely one which whose existence is
necessary. By our understanding of the essential properties of God as
developed above, it is impossible to conceive of a being greater than God.
Perhaps a more modern language would help in thinking about Axiom 2. Anselm
is saying, in effect, that if God existed contingently, but not necessarily,
then we could ask questions like "If God made the universe, then who made
God?" A being invoked to explain the existence of
the universe, but whose existence is in need of explanation,
is not great enough for Anselm to call God.
Anselm's basic idea was that God has a property that other individuals lack,
namely maximal greatness or perfection. Imagine that you, like the great
Italian poet Dante, were lifted up in a dream for a personal interview
with God. Having explained to you how she created the universe, and
explained the answers to mysterious questions in quantum mechanics and
particle physics, you finally get around to asking the following question:
"OK God, you've explained to me how you made the universe. So I know
where the universe comes from and why it is the way it is. But where do
you come from?" If God answered "Gee, I don't know" you would feel
disappointed I suspect. You would feel that God is not as knowledgeable
as you would like. Anselm's insight was that a God who could answer this
question (even if we did not understand the answer) would be a greater God
than one who could not. Since God, by definition, is maximally great, she
should have an answer. To say there can be no answer is to say that
Anselm's God necessarily does not exist. To say that there is an answer
is to say that necessarily Anselm's God exists. (Note that I am careful
to speak only of Anselm's God here. Others have seen God in different
terms.) Since God is maximally great, she must be self-creating, i.e.,
have the source of all existence (including her own existence) within
herself.
[As a technical aside, we should note the affinity between this step of
Anselm's argument, and certain reasoning in the cosmological
argument for God's existence. The principle of sufficient
reason implies that in order for the universe to have a
first cause, namely God, the first cause must be a "self-causing
cause." If not, then God would have a prior cause. But a
self-causing cause -- one which contains the explanation for its own
existence -- is rather like a necessarily existing being. The similarity
between the arguments should not be overstated: belief in one argument
does not entail belief in the other. For
example, Thomas Aquinas accepted
the cosmological argument but not the ontological argument for God.]
Now let us consider the ramifications of Axioms 1 and 2 within the modal logic
S5.
1. g 
 g (Axiom 2)
g (Axiom 2)
2.  ~g
~g 

 ~g
(Becker postulate 2)
~g
(Becker postulate 2)
3.  g
g 
 ~g (law of excluded middle)
~g (law of excluded middle)
4.  g
g 

 ~g (2, 3 using substitution rule)
~g (2, 3 using substitution rule)
5.  ~g
~g  ~g (contrapositive
of Axiom 2)
~g (contrapositive
of Axiom 2)
6.  (
(  ~g
~g
 ~g) (necessitation postulate on 5)
~g) (necessitation postulate on 5)
7. 
 ~g
~g

 ~g
(modus ponens on 6)
~g
(modus ponens on 6)
8.  g
g 
 ~g (substitution rule on 4 and 7)
~g (substitution rule on 4 and 7)
9. ~ ~g (Axiom 1)
~g (Axiom 1)
10.  g (8 and 9)
g (8 and 9)
This is the modern form of Anselm's ontological argument, due to
Charles Hartshorne. Anselm himself
did not have the full power of S5 available to him. So his
argument is not exactly the same as this. However, the basic idea of
both arguments is that
necessary existence is an essential property of God entailed by God's
greatness.
We must either accept the conclusion of the argument, namely that God
exists necessarily, or find fault with an axiom or postulate. Critical
scrutiny has been brought to bear on the following parts of the argument:
- Becker's postulate
- Axiom 2
- Axiom 1
While there was initially some suspicion of Becker's postulate and the modal
logic S5, the dust seems to have settled on this. We now know
that there is nothing particularly remarkable about the assumptions of
S5. While Becker's postulate is not required in other types
of modal logic, Saul Kripke's possible world semantics have interpreted
Becker's postulate for us. If we imagine that two individuals from
different possible worlds were
able to compare their understanding of the meaning of  ,
then Becker's postulate is a statement of equivalence in their
interpretations of
,
then Becker's postulate is a statement of equivalence in their
interpretations of  . We might imagine, for example, that
a Napoleon who won the battle of Waterloo was able to sit down at the table
with a Napoleon who lost the battle of Waterloo to discuss how the battle
went. If Becker's postulate is satisfied, then they should be able to
agree about which contingencies are truly possible.
This seems to be most closely in accord with our naive views of modal
possibility. That is not to say that it is forced upon us.
. We might imagine, for example, that
a Napoleon who won the battle of Waterloo was able to sit down at the table
with a Napoleon who lost the battle of Waterloo to discuss how the battle
went. If Becker's postulate is satisfied, then they should be able to
agree about which contingencies are truly possible.
This seems to be most closely in accord with our naive views of modal
possibility. That is not to say that it is forced upon us.
In the absence of anything outrageously wrong with S5, we can
turn to the two axioms. Axiom 2 has come under a lot of scrutiny. However,
many of the arguments have lost their force. In the original version of
the argument, Anselm claimed that contingent existence is greater than possible
existence, and that necessary existence is greater than contingent existence.
 This seems to treat existence as just another property of individuals, such
as whether they are wearing red suits or have white beards.
Immanuel Kant (1724-1804)
criticized the ontological argument by stating that existence is not a
predicate. That is, existence is not a property of individuals in the same
way that being short or red is. It is certainly true that we have to be
careful here. If we can arbitrarily add existence as a defining property for
an individual, there seems to be no limit to what we can prove to exist. For
example, we might define a unicorn as follows:
This seems to treat existence as just another property of individuals, such
as whether they are wearing red suits or have white beards.
Immanuel Kant (1724-1804)
criticized the ontological argument by stating that existence is not a
predicate. That is, existence is not a property of individuals in the same
way that being short or red is. It is certainly true that we have to be
careful here. If we can arbitrarily add existence as a defining property for
an individual, there seems to be no limit to what we can prove to exist. For
example, we might define a unicorn as follows:
Definition:
A unicorn is a four-footed beast resembling a horse having a horn on its
head and existing.
Thus unicorns exist. By definition.
However, this is a parody of Anselm's argument, and doesn't stand up under
close examination. Any good mathematician will allow you (within reason) to
define your terms any way that you like. So there is nothing wrong with the
definition. Can we really show that unicorns exist using this argument?
The answer is no.
Our definition of a unicorn would only seem to imply that
all unicorns exist, or equivalently,
that for all x, if x is a unicorn then x exists. However,
this statement is trivially true, because it is vacuously satisfied.
Anyway, the form of the
ontological argument that we have used does not explicitly assume that
existence is a predicate. It assumes that the modal status of
an individual (the Eiffel tower, say, or the number 17) can be regarded as a
property. A number between 16 and 18 exists necessarily, whereas
the Eiffel tower exists contingently, and the distinction between the two
can be regarded as a property of each.
The statements
(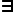 x) (16 < x < 18)
x) (16 < x < 18) 
 (
(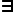 x) (16 < x < 18)
x) (16 < x < 18)
and
(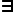 x) (18 < x < 16)
x) (18 < x < 16) 
 (
(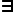 x) (18 < x < 16)
x) (18 < x < 16)
are both true in the domain of natural numbers because natural numbers are
Platonic objects. (The latter is also true vacuously.)
Both these statements are reasonable mathematically, and
parallel to Axiom 2.
Therefore Axiom 2 cannot be easily dismissed.
For my money, the real problem with Anselm's ontological argument is Axiom 1.
I have argued that the reasons given for believing Axiom 1 are not correct
because they confuse statements which are possibly true
with statements which are
conceivably true. If we remove Axiom 1 from the argument, then we are still
able to prove the statement
 g
g 
 g
g
namely, that the possibility of God's existence implies the necessity of
God's existence. But we can prove no more than this. Many philosophers who
have studied the ontological argument are willing to accept that Anselm's
reasoning can take us this far and no further. While the jump from possible
existence to necessary existence would seem to be useful, we should remember
that if the statement g is interpreted as any mathematical statement, true
or false, about the natural numbers, then the statement is true as well. It
may be a bit of a stretch to declare that Anselm has demonstrated that God,
like the smallest even integer greater than two which cannot be represented
as the sum of two primes, is a Platonic entity. However, in the broad sense,
that is what he accomplished.
It was Gödel who tackled the problem of possible existence head on.
Before we consider his proof, it should be pointed out that much of Gödel's
argument is inspired by the writings of Leibniz on the subject.
Leibniz argued that the weakness of Anselm's argument is
in the statement of God's possible existence. Gödel's argument
follows Leibniz in bolstering this step with additional argumentation.
Reader's who are familiar with Leibniz's ontological argument may find
echoes of Leibniz's method of affirmative simples in Gödel's work.


![[BACK]](home.gif) Back to Christopher Small's home page .
Back to Christopher Small's home page .
 Anselm of Aosta (1033-1109) should
also be understood in this context. Like Abelard
or Hildegard, Anselm was a brilliant man whose natural vocation was within
the medieval Church. His biographers have referred to the transformation
that he introduced as the "Anselmian revolution." While he is best
known outside ecclesiastical circles for his ontological argument, his
influence on religious writing is every bit as important. Anselm invented a
new form of poetry -- the poetry of personal devotion written in rhymed Latin
with intricate logical structure and antitheses.
Anselm of Aosta (1033-1109) should
also be understood in this context. Like Abelard
or Hildegard, Anselm was a brilliant man whose natural vocation was within
the medieval Church. His biographers have referred to the transformation
that he introduced as the "Anselmian revolution." While he is best
known outside ecclesiastical circles for his ontological argument, his
influence on religious writing is every bit as important. Anselm invented a
new form of poetry -- the poetry of personal devotion written in rhymed Latin
with intricate logical structure and antitheses.
 g
g

 g
g

 This seems to treat existence as just another property of individuals, such
as whether they are wearing red suits or have white beards.
Immanuel Kant (1724-1804)
criticized the ontological argument by stating that existence is not a
predicate. That is, existence is not a property of individuals in the same
way that being short or red is. It is certainly true that we have to be
careful here. If we can arbitrarily add existence as a defining property for
an individual, there seems to be no limit to what we can prove to exist. For
example, we might define a unicorn as follows:
This seems to treat existence as just another property of individuals, such
as whether they are wearing red suits or have white beards.
Immanuel Kant (1724-1804)
criticized the ontological argument by stating that existence is not a
predicate. That is, existence is not a property of individuals in the same
way that being short or red is. It is certainly true that we have to be
careful here. If we can arbitrarily add existence as a defining property for
an individual, there seems to be no limit to what we can prove to exist. For
example, we might define a unicorn as follows:
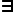 x) (16 < x < 18)
x) (16 < x < 18) 

![[BACK]](home.gif) Back to Christopher Small's home page .
Back to Christopher Small's home page .